Word Error Rate in Python

Confused by complex code? Let our AI-powered Code Explainer demystify it for you. Try it out!

Word Error Rate (WER) is a metric commonly used to evaluate the accuracy of automatic speech recognition (ASR) systems or machine translation systems.

When converting spoken words to written text, errors such as missing words, adding extra words, or misinterpreting words can occur. WER measures the difference between the original and recognized or translated texts. It calculates the number of substitutions, deletions, and insertions required to transform the recognized or translated text into the reference text, normalized by the total number of words in the reference text.

• How WER is Calculated
• Implementation of WER in Python
• An Accurate Way to Calculate WER
• WER with JiWER Library
• WER with Evaluate Library
• Conclusion

How WER is Calculated

The formula to calculate WER is as follows:

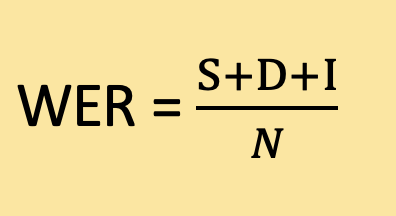where:

• S is the number of word substitutions. A substitution occurs when a word in the recognized or translated text is different from the corresponding word in the reference text.
• D is the number of word deletions. A deletion occurs when a word in the reference text is missing from the recognized or translated text.
• I is the number of word insertions. An insertion occurs when an extra word is present in the recognized or translated text that is not in the reference text.
• N is the total number of words in the reference text.

Example:

Reference text: "The cat is sleeping on the mat."

Recognized text: "The cat is playing on mat."

To calculate the WER, we need to identify the number of substitutions, deletions, and insertions.

Substitutions:

In this example, there is a one-word substitution:

"playing" instead of "sleeping"

Deletions:

There is a one-word deletion:

"the" before "mat"

Insertions:

There are no word insertions in this example.

Total number of words in the reference text (N): 7

Using the formula, we can calculate the WER:

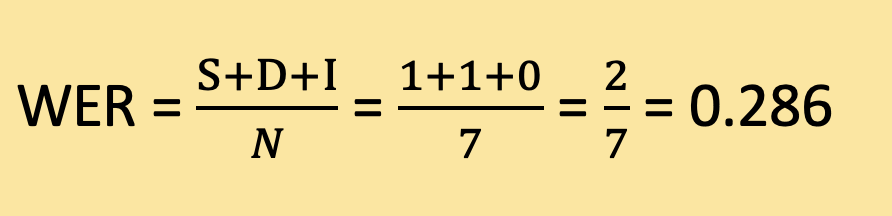
Therefore, the Word Error Rate for this example is approximately 0.286 or 28.6%. This means that out of the total words in the reference text, around 28.6% were either substituted or deleted in the recognized text.

Implementation of WER in Python

Let's implement WER in Python from scratch:

def calculate_wer(reference, hypothesis):
	ref_words = reference.split()
	hyp_words = hypothesis.split()
	# Counting the number of substitutions, deletions, and insertions
	substitutions = sum(1 for ref, hyp in zip(ref_words, hyp_words) if ref != hyp)
	deletions = len(ref_words) - len(hyp_words)
	insertions = len(hyp_words) - len(ref_words)
	# Total number of words in the reference text
	total_words = len(ref_words)
	# Calculating the Word Error Rate (WER)
	wer = (substitutions + deletions + insertions) / total_words
	return wer

This calculate_wer() function takes two parameters: reference and hypothesis sentences. These parameters represent the reference text (ground truth) and the hypothesis text (recognized or translated text).

The function first splits the reference and hypothesis strings into individual words using the split() method. This creates two lists: ref_words containing the words from the reference text, and hyp_words containing the words from the hypothesis text.

Next, the function counts the number of substitutions, deletions, and insertions. It uses a generator expression with the zip() function to iterate over corresponding pairs of words from ref_words and hyp_words. The condition ref != hyp checks if the words are different, and the sum(1 for ...) counts the number of times this condition is true, giving us the number of substitutions.

The number of deletions is calculated by subtracting the length of hyp_words from the length of ref_words. Similarly, the number of insertions is calculated by subtracting the length of ref_words from the length of hyp_words.

The total number of words in the reference text is obtained by using the len() function on ref_words.

Finally, the Word Error Rate (WER) is calculated by summing the substitutions, deletions, and insertions and dividing it by the total number of words in the reference text.

Example demonstration of the above function:

reference_text = "The cat is sleeping on the mat."
hypothesis_text = "The cat is playing on mat."
 
wer_score = calculate_wer(reference_text, hypothesis_text)
print("Word Error Rate (WER):", wer_score)

In this example, the calculate_wer() function is called with the reference text "The cat is sleeping on the mat." and the hypothesis text "The cat is playing on mat." The resulting WER score is stored in the variable wer_score. Finally, the WER score is printed.

Output:

Word Error Rate (WER): 0.2857142857142857

The resulting WER is approximately 0.286 or 28.6% for the given example.

An Accurate Way to Calculate WER

Our current function does not accurately compute the WER. One issue is how substitutions, deletions, and insertions are counted, especially when the lengths of the reference and hypothesis sentences are different. Here, if one sentence is longer than the other, the zip() function will only pair words up to the length of the shorter sentence, and any additional words are not considered. We could use the zip_longest() from itertools module, but we're going to use a completely different approach.

We need a dynamic programming approach to this problem, such as the Levenshtein distance. Here is a simple Python function implementing the Levenshtein distance algorithm, which is a more appropriate way to calculate WER:

import numpy as np

def calculate_wer(reference, hypothesis):
    # Split the reference and hypothesis sentences into words
    ref_words = reference.split()
    hyp_words = hypothesis.split()
    # Initialize a matrix with size |ref_words|+1 x |hyp_words|+1
    # The extra row and column are for the case when one of the strings is empty
    d = np.zeros((len(ref_words) + 1, len(hyp_words) + 1))
    # The number of operations for an empty hypothesis to become the reference
    # is just the number of words in the reference (i.e., deleting all words)
    for i in range(len(ref_words) + 1):
        d[i, 0] = i
    # The number of operations for an empty reference to become the hypothesis
    # is just the number of words in the hypothesis (i.e., inserting all words)
    for j in range(len(hyp_words) + 1):
        d[0, j] = j
    # Iterate over the words in the reference and hypothesis
    for i in range(1, len(ref_words) + 1):
        for j in range(1, len(hyp_words) + 1):
            # If the current words are the same, no operation is needed
            # So we just take the previous minimum number of operations
            if ref_words[i - 1] == hyp_words[j - 1]:
                d[i, j] = d[i - 1, j - 1]
            else:
                # If the words are different, we consider three operations:
                # substitution, insertion, and deletion
                # And we take the minimum of these three possibilities
                substitution = d[i - 1, j - 1] + 1
                insertion = d[i, j - 1] + 1
                deletion = d[i - 1, j] + 1
                d[i, j] = min(substitution, insertion, deletion)
    # The minimum number of operations to transform the hypothesis into the reference
    # is in the bottom-right cell of the matrix
    # We divide this by the number of words in the reference to get the WER
    wer = d[len(ref_words), len(hyp_words)] / len(ref_words)
    return wer

Let's use it:

if __name__ == "__main__":
    reference = "The cat is sleeping on the mat."
    hypothesis = "The cat is playing on mat."
    print(calculate_wer(reference, hypothesis))

0.2857142857142857

WER with JiWER Library

We can use the JiWER library to calculate WER in Python, let's install it:

$ pip install jiwer

Open up a new Python file and add the following:

from jiwer import wer

if __name__ == "__main__":
    reference = "The cat is sleeping on the mat."
    hypothesis = "The cat is playing on mat."
    print(wer(reference, hypothesis))

0.2857142857142857

WER with Evaluate Library

If you're particularly using Huggingface libraries such as 🤗 Transformers, you may want to use their 🤗 Evaluate library to calculate the WER:

import evaluate

wer = evaluate.load("wer")

reference = "The cat is sleeping on the mat."
hypothesis = "The cat is playing on mat."
print(wer.compute(references=[reference], predictions=[hypothesis]))

0.2857142857142857

Conclusion

In conclusion, Word Error Rate (WER) is a valuable tool for evaluating the accuracy of automatic speech recognition (ASR). It calculates the number of errors in the recognized or translated text, accounting for substitutions, deletions, and insertions.

In this tutorial, we have explored WER, as well as implemented it in raw Python using the Levenshtein distance. We also saw how to calculate it using JiWER and 🤗 evaluate libraries in Python.

It's worth noting that while WER is a common metric, it is not without limitations. For instance, it assumes that each word's importance in a sentence is the same, which might not always be true in certain contexts. In such cases, other evaluation metrics might be more suitable. However, WER remains a good starting point for assessing the performance of ASR or machine translation systems.

You can get the complete codes for this tutorial here.

Learn also: How to Calculate the BLEU Score in Python.

Happy coding ♥

Found the article interesting? You'll love our Python Code Generator! Give AI a chance to do the heavy lifting for you. Check it out!

Read Also

How to Calculate the BLEU Score in Python

Deep-dive into the BLEU Score: A guide to understanding BLEU (Bilingual Evaluation Understudy), a vital metric in NLP. Learn how it evaluates machine-generated sentences against human references in text summarization, translation, and more with NLTK in Python.

Speech Recognition in Python

Learn how to do Automatic Speech Recognition (ASR) using APIs and/or directly performing Whisper inference on Transformers in Python

Image Captioning using PyTorch and Transformers in Python

Learn how to use pre-trained image captioning transformer models and what are the metrics used to compare models, you'll also learn how to train your own image captioning model with Pytorch and transformers in Python.

Comment panel